힐베르트 변환
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
힐베르트 변환은 함수와 코시 커널의 합성곱으로 정의되며, 신호 처리, 통신, 수학 등 다양한 분야에서 활용된다. 1905년 다비트 힐베르트의 연구에서 시작되었으며, 푸리에 변환 영역에서 곱셈 연산자로 작용하여 신호의 위상을 변경한다. 힐베르트 변환은 유계 선형 연산자이며, 이산 신호에 대한 이산 힐베르트 변환도 존재한다. 해석적 신호 표현, 단측파대 변조, 각 변조 등 다양한 응용 분야에서 활용되며, 특정 함수의 힐베르트 변환은 표로 정리되어 있다.
더 읽어볼만한 페이지
- 적분 변환 - 라플라스 변환
라플라스 변환은 함수 f(t)를 복소수 s를 사용하여 적분을 통해 다른 함수 F(s)로 변환하는 적분 변환이며, 선형성을 가지고 미분방정식 풀이 등 공학 분야에서 널리 사용된다. - 적분 변환 - 푸리에 변환
푸리에 변환은 복소 함수를 주파수 성분으로 분해하는 적분 변환으로, 푸리에 급수의 확장 개념이며, 시간-주파수 영역 변환, 선형성, 컨볼루션 정리, 불확정성 원리 등의 성질을 가지며 다양한 분야에 활용된다. - 조화 함수 - 라플라스 방정식
라플라스 방정식은 리만 다양체에서 라플라스-벨트라미 연산자의 2차 편미분 방정식이며, 조화 함수를 해로 갖고 유체 역학, 정전기학 등 다양한 분야에 응용된다. - 조화 함수 - 코시-리만 방정식
코시-리만 방정식은 복소해석학에서 함수가 미분 가능하기 위한 조건을 제공하며, 복소 평면에서 정의된 함수가 정칙 함수가 되기 위한 필요충분조건과 관련된다. - 다비트 힐베르트 - 힐베르트 공간
힐베르트 공간은 내적 공간이면서 내적으로부터 유도된 거리 함수에 대해 완비 거리 공간을 이루는 공간으로, 다양한 함수 공간의 예시를 가지며 푸리에 해석, 양자역학 등 여러 분야에 응용된다. - 다비트 힐베르트 - 힐베르트 기저 정리
힐베르트 기저 정리는 가환환 R이 뇌터 환일 때 R을 계수로 하는 다항식환 R[x_1,...,x_n] 역시 뇌터 환임을 명시하는 정리이며, 대수기하학에서 대수적 집합을 유한 개의 다항식의 공통근으로 해석할 수 있게 한다.
2. 역사
힐베르트 변환은 1905년 다비트 힐베르트가 리만이 제시한 해석 함수에 관한 문제에 대한 연구에서 비롯되었다. 힐베르트의 연구는 주로 원 위에 정의된 함수에 대한 힐베르트 변환에 관한 것이었다. 그의 초기 연구 중 일부는 그가 괴팅겐에서 했던 강의와 관련된 이산 힐베르트 변환으로 거슬러 올라간다. 그 결과는 후에 헤르만 바일에 의해 그의 논문에서 발표되었다.[1] 슈르는 이산 힐베르트 변환에 대한 힐베르트의 결과를 개선하고 적분 형태로 확장했다.[2] 이러한 결과는 Lp 공간으로 제한되었다. 1928년, 마르첼 리즈는 힐베르트 변환이 (Lp 공간)에서 ''u''에 대해 1 < ''p'' < ∞로 정의될 수 있으며, 힐베르트 변환은 에서 1 < ''p'' < ∞에 대한 유계 연산자이고, 원에 대한 힐베르트 변환과 이산 힐베르트 변환에 대해서도 유사한 결과가 성립함을 증명했다.[3] 힐베르트 변환은 안토니 지그문트와 알베르토 칼데론이 특이 적분에 대한 연구를 하는 동안 동기 부여가 되는 예시였다.[4] 그들의 연구는 현대 조화 해석에서 기본적인 역할을 했다. 쌍선형 및 삼선형 힐베르트 변환과 같은 힐베르트 변환의 다양한 일반화는 오늘날에도 여전히 활발히 연구되는 분야이다.
''u''(''t'')의 힐베르트 변환은 함수 ''h''(''t'') = 1/(π''t'')영어와 ''u''(''t'')의 합성곱으로 생각할 수 있다. ''h''(''t'')는 적분할 수 없기 때문에, 합성곱을 정의하는 적분은 수렴하지 않는다. 대신, 코시 주요값(p.v.로 표시)을 사용하여 힐베르트 변환을 정의한다. 명시적으로, 함수 또는 신호 ''u''(''t'')의 힐베르트 변환은 다음과 같다.[1]
힐베르트 변환은 푸리에 변환 영역에서 곱셈 연산자로 작용한다. 즉, 신호의 힐베르트 변환은 해당 신호의 푸리에 변환에 -''i'' sgn(ω)를 곱한 것과 같다. 여기서 sgn(ω)은 부호 함수이다.
힐베르트 변환은 인 공간에서 유계 선형 연산자이다.[8] 즉, 모든 에 대해 다음 부등식을 만족하는 상수 가 존재한다.
3. 정의
:
변수 변환을 통해 다음과 같이 쓸 수도 있다.[2]
:
4. 푸리에 변환과의 관계
:
오일러 공식에 의해,
:
따라서 힐베르트 변환 ''H''(''u'')(''t'')는 ''u''(''t'')의 음의 주파수 성분은 위상을 +90° (π/2 라디안) 이동시키고, 양의 주파수 성분은 위상을 -90° 이동시키는 효과를 갖는다.
5. 성질
:
이때 최적 상수 는 다음과 같이 주어진다.[9]
:
주기적 힐베르트 변환에서도 동일한 최적 상수가 성립한다.
힐베르트 변환은 반 자기 수반 연산자[10]이므로, 다음이 성립한다.
:
또한, 힐베르트 변환은 반대합이므로, 힐베르트 변환을 두 번 적용하면 원래 함수의 부호가 반전된다.
:
이는 힐베르트 변환이 가역적이며, 다음 관계가 성립함을 의미한다.
:
실수 바나흐 공간에서 힐베르트 변환은 선형 복소 구조를 정의한다. 특히, 일 때 힐베르트 변환은 의 실수 값 함수로 구성된 힐베르트 공간에 복소수 힐베르트 공간의 구조를 부여한다.
힐베르트 변환의 도함수는 도함수의 힐베르트 변환과 같다. 즉, 다음이 성립한다.
:
이를 반복하면, 다음 관계를 얻는다.
:
힐베르트 변환은 형식적으로 다음과 같이 convolution영어으로 표현될 수 있다.
:
여기서 이다. 대부분의 경우 힐베르트 변환은 합성곱으로 취급될 수 있다. 예를 들어, 다음이 성립한다.
:
힐베르트 변환은 변환, 양수 팽창과 교환하며, 반사와는 반교환한다.
5. 1. 이산 힐베르트 변환
이산 시간 푸리에 변환(DTFT)을 이용하여 이산 신호 에 대한 이산 힐베르트 변환을 정의할 수 있다. 은 다음과 같이 표현된다.[42]
:
여기서:
:
합성곱 정리에 의해, 위 식은 다음과 같이 바꿔 쓸 수 있다.
:
여기서:
:
이산 힐베르트 변환은 FIR 필터 또는 DFT를 이용하는 방법으로 구현할 수 있다.[42]
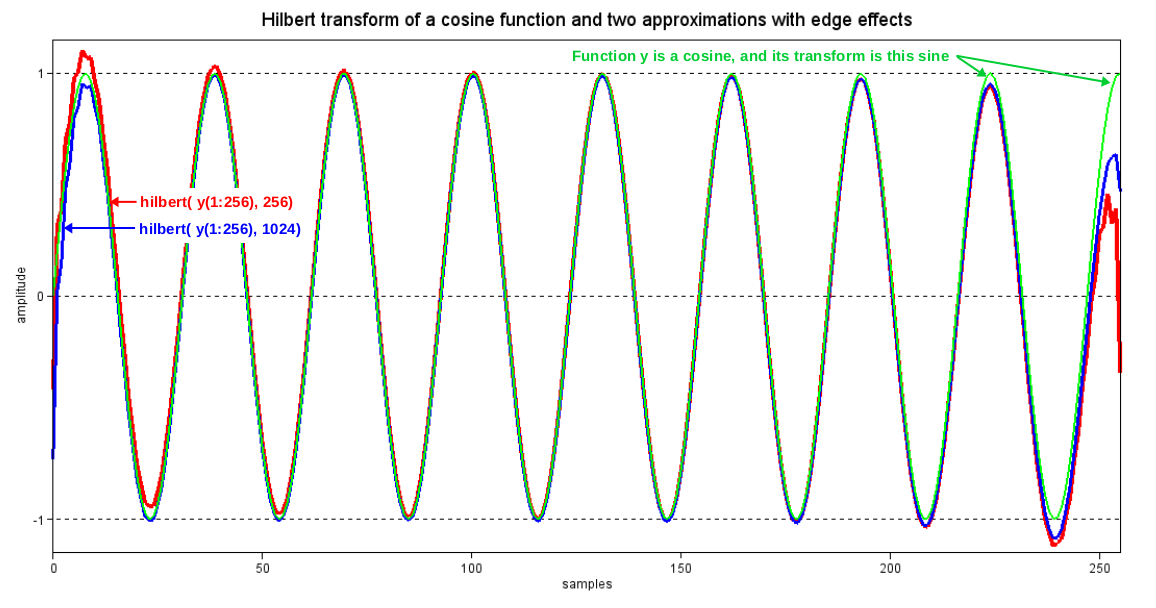
매트랩의 `hilbert(u, N)` 함수는 의 근사 이산 힐베르트 변환을 복소수 출력의 허수 부분으로 계산한다. 실수 부분은 원래 입력 데이터이므로, 복소수 출력은 의 해석적 표현이 된다. `hilbert(u, N)` 함수는 과의 합성곱을 사용하며, 출력 데이터 수를 무시하고 값을 크게 하여 왜곡을 줄일 수 있다. '''그림 4'''는 이러한 왜곡의 예를 보여준다.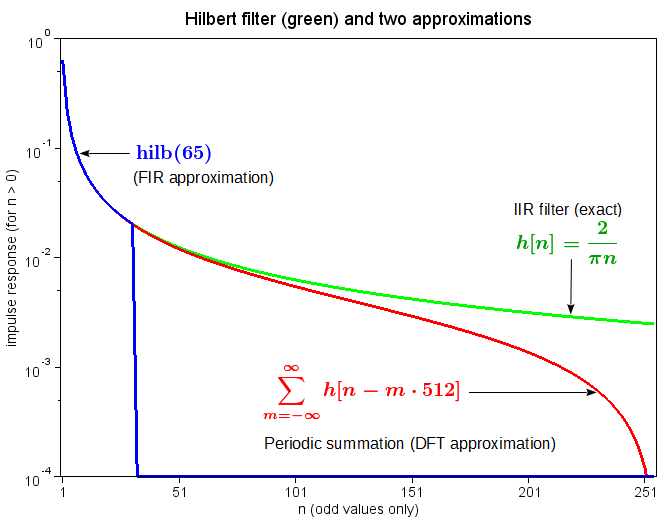
6. 응용
힐베르트 변환은 다양한 신호 처리 분야에서 응용된다.
- '''해석적 신호 표현:''' 힐베르트 변환은 실수 신호로부터 해석적 신호를 생성하는 데 사용된다. 해석적 신호는 신호의 진폭과 위상 정보를 분리하여 분석하는 데 유용하다.
- '''단측파대 변조 (SSB):''' 힐베르트 변환은 단측파대 변조 방식에서 중요한 역할을 한다.[17][18]
- '''각 변조:''' 힐베르트 변환은 각 변조된 신호의 순시 주파수 및 위상을 추정하는 데 사용될 수 있다.[16]
- '''베드로시안 정리:''' 이 정리에 따르면, 겹치지 않는 스펙트럼을 갖는 저역 통과 신호와 고역 통과 신호의 곱에 대한 힐베르트 변환은 각 신호의 힐베르트 변환의 곱으로 주어진다.[15]
7. 확장
힐베르트 변환은 다음과 같은 분포 공간으로 확장될 수 있다.
- 분포 공간에서의 힐베르트 변환: 힐베르트 변환은 미분과 교환 가능하며, 에서 유계 연산자이므로, 소볼레 공간의 역극한에 대한 연속 변환을 제공한다. 이를 통해 분포로 구성된 공간에서 힐베르트 변환을 정의할 수 있다.[1]
- 유계 평균 진동 함수 (BMO) 공간에서의 힐베르트 변환: 함수에 대한 힐베르트 변환은 유계 평균 진동(BMO) 클래스로 매핑된다. 이 변환은 정칙화된 형태로 정의되며, 컴팩트한 지지 집합을 가진 함수에 대해 원래 변환과 덧셈 상수까지 일치한다.[12]
- 원형 힐베르트 변환: 주기 함수에 대한 힐베르트 변환은 다음과 같이 정의된다.
이는 하디 공간의 특성 부여와 푸리에 급수에서의 켤레 함수 연구에 사용된다.
- 수론적 힐베르트 변환: 이산 힐베르트 변환은 수론적 변환으로 확장될 수 있다. 이는 이산 푸리에 변환을 수론적 변환으로 일반화하는 것을 따르며, 직교 이산 수열 집합을 생성하는 데 사용될 수 있다.
8. 특정 함수의 힐베르트 변환 (표)
참조
[1]
참고문헌
[2]
참고문헌
[3]
참고문헌
[4]
참고문헌
[5]
참고문헌
[6]
인용
[7]
설명
[8]
참고문헌
[9]
참고문헌
[10]
참고문헌
[11]
참고문헌
[12]
참고문헌
[13]
참고문헌
[14]
참고문헌
[15]
참고문헌
[16]
참고문헌
[17]
참고문헌
[18]
참고문헌
[19]
참고문헌
[20]
참고문헌
[21]
참고문헌
[22]
참고문헌
[23]
참고문헌
[24]
참고문헌
[25]
참고문헌
[26]
참고문헌
[27]
참고문헌
[28]
참고문헌
[29]
참고문헌
[30]
참고문헌
[31]
참고문헌
[32]
참고문헌
[33]
참고문헌
[34]
웹사이트
hilbert – Discrete-time analytic signal using Hilbert transform
http://www.mathworks[...]
2021-05-06
[35]
참고문헌
[36]
서적
Stein Weiss
1971
[37]
서적
Bracewell
2000
[38]
서적
Bracewell
2018-09
[39]
문서
sin cos의 힐베르트 변환
[40]
서적
Brace Well
[41]
문서
sin과 cos 함수의 힐버트 변환
[42]
서적
Grafakos
1994
[42]
서적
Titchmarsh
1926
[42]
서적
Hardy Littlewood Polya
1952
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com